JMO2021予選 第5問、第6問
以前の記事の続きをする。
この年の予選通過点は6点だったため、前回までの4問と、今回の2問を解けば合格だ。
5.以下のように図形に記号を割り振る。

2*2*1の長方形に埋める問題を考える。Dのみしかできないので、1通り。
次に、2*2*2の長方形に埋める問題を考えてみよう。
4通りある。1)Aのみ、2)Bのみ、3)Cのみ、4)Dのみ、を使う方法だ。
1)回転のさせ方を考えて、4通り。上に出っ張ってるのが、どこかで4通り。
2)底面に注意する。上に1つ出っ張るのが、4通り。上に2つ出っ張るのが、2通り。よって、6通り。
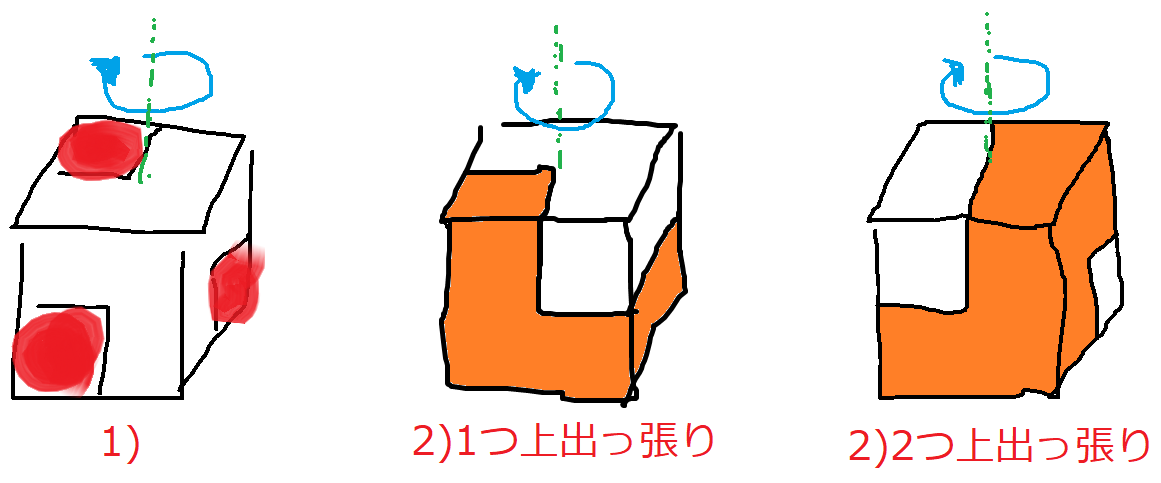
3)2)と同様に、6通り。
4)水平に重ねるのは、1通り。2枚垂直積むのは、2通り。よって、3通り。
合計で、4+6+6+3=19通り。
2*2*4の長方形を埋める方法のうち、2*2*2の2つではっきり分割出来るものは、19^2=361通り。
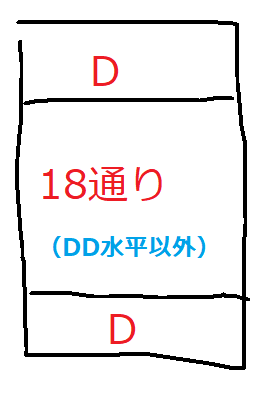
分けられないときのうち、一番上の層と、一番下の層がDで水平に重なりつつ、間の二番目と三番目の層が、Dの水平積み上げ以外のもの、は、18通り。DD水平積み上げを除く理由は、上下の2段に分割出来てしまい、上の361通りで既にカウントされているから。
よって、361+18=379通り
6.f(1)=2, f(2)=1, f(3)=2,...。というように実験していくと、気づくことがある。
以下の方法が、使えることがわかる。
n+1が、k未満の素数(または1)の全てで割り切れ、kで割り切れない数だとする。kはk未満の素数で割りきれないので、kは素数。そして、n+1がk未満の全ての素数を割りきるので、(n+1とnが互いに素であることから、)nがk未満の全ての素数で割りきれない。よって、nとk-1が互いに素である。だから、f(n)=k-1、となる。
あらゆるn+1に対して、kは存在するので、それを見つける方法を次に探す。
例えば、2とも3とも5とも互いに素でない、最初の整数は、30である。よって、次の素数7は、30と互いに素となる。先述の方法を適応すると、f(29)=7-1=6 となる。30未満の数は、全て2か3か5かいずれかと互いに素となるので、その3つの数だけに注意すれば良い。
このように考えると、10^10+1以下の整数が、どの素数以下の素数と互いに素か、を考える問題に落ち着く。よって、素数を小さいものから掛けて、10^10を超えた時に掛けた回数を考える。2*3*5*7*11*13*17*19*23*27<10^10<2*3*5*7*11*13*17*19*23*27*29より、11回掛けている。よって、11種類
これで予選合格だ。嬉しい。