クロソイド曲線 - 医科学(仮)

自動車を運転することがある。
その際に、高速道路の上を運転することがある。
高速道路は、まっすぐの道以外にも、曲がりくねった道がある。
その曲がり方に関わりがあるのが、クロソイド曲線だ
- 知りたい。
始めましょうか。
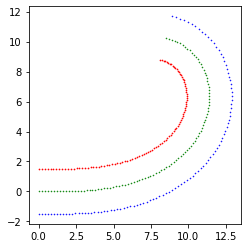
クロソイド曲線
- 曲率を一定割合で変化させた時に、描かれる軌跡がクロソイド曲線
  - 性質
    - 曲率半径と始点からの曲線長の積が一定
      - $RL = A^2$
      - 最初はまっすぐ。だんだんカーブきつくなる。そして、円っぽく。
    - 相似
      - Aで二変数を割る
- 座標的な情報
  - $x(l) = \int cos(\theta^2 /2 )d \theta$
  - $y(l) = \int sin(\theta^2 /2 )d \theta$
  - フレネル積分
    - 光の回折の仕方
      - フレネル回折
    - 複素解析
      - 複素平面全領域で正則
      - $\int dz e^{iz^2}$ の扇形積分
      - 0から∞で、 $\sqrt{\frac{\pi}{8}}$
- 曲率
  - 曲率が0のものが直線
  - 有限値のものが円
- 道
  - ハンドルを一定の角速度で回すと、自動車が描く曲線
    - 高速道路で、直線道路から円道路に移行する間の緩和曲線
    - 急なハンドル操作が要らない
    - 躍度を抑える
    - クロソイド曲線区間の走行時間が3秒以上
お絵かきしてみる。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import math 

# figureを生成する
fig = plt.figure()
# axをfigureに設定する
ax = fig.add_subplot(1, 1, 1)

D = 3;v = 200
T = 100;k = 0.0003;dt = 0.001
x1 = [0 for i in range(T)]
x2 = [0 for i in range(T)]
x3 = [0 for i in range(T)]
y1 = [0 for i in range(T)]
y2 = [0 for i in range(T)]
y3 = [0 for i in range(T)]
z = [0 for i in range(T)]

y2[0] = D/2
y3[0] = -D/2
for t in range(T-1):
  x1[t+1] = x1[t] + v *math.cos(k*t**2)*dt
  y1[t+1] = y1[t] + v *math.sin(k*t**2)*dt
  x2[t+1] = x1[t+1] - D/2*math.sin(k*t**2)
  y2[t+1] = y1[t+1] + D/2*math.cos(k*t**2)
  x3[t+1] = x1[t+1] + D/2*math.sin(k*t**2)
  y3[t+1] = y1[t+1] - D/2*math.cos(k*t**2)

# axesに散布図を設定する
ax.scatter(x1, y1, s=0.3, c='g')
ax.scatter(x2, y2, s=0.5, c='r')
ax.scatter(x3, y3, s=0.3, c='b')
# 表示する
plt.show()

f:id:medical-science:20220228000343p:plain — 車幅3ｍ

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import math 

# figureを生成する
fig = plt.figure()
# axをfigureに設定する
ax = fig.add_subplot(1, 1, 1)

D = 3;v = 200;h = 1.5
b = 1#車の先端から目の距離
T = 100;k = 0.0003;dt = 0.001
x1 = [0 for i in range(T)]
x2 = [0 for i in range(T)]
x3 = [0 for i in range(T)]
y1 = [0 for i in range(T)]
y2 = [0 for i in range(T)]
y3 = [0 for i in range(T)]
z = [0 for i in range(T)]

y2[0] = D/2
y3[0] = -D/2
for t in range(T-1):
  x1[t+1] = x1[t] + v *math.cos(k*t**2)*dt
  y1[t+1] = y1[t] + v *math.sin(k*t**2)*dt
  x2[t+1] = x1[t+1] - D/2*math.sin(k*t**2)
  y2[t+1] = y1[t+1] + D/2*math.cos(k*t**2)
  x3[t+1] = x1[t+1] + D/2*math.sin(k*t**2)
  y3[t+1] = y1[t+1] - D/2*math.cos(k*t**2)


def Eye(x,y,z):
  r = math.sqrt(y**2+z**2)
  theta = math.atan2(r,abs(x))
  phi = math.atan2(z,y) 
  #return [math.sin(theta)*math.cos(phi),math.sin(theta)*math.sin(phi)]
  return [-theta*math.cos(phi),theta*math.sin(phi)]
  #return [theta,phi]


x4 = [0 for i in range(T)]
x5 = [0 for i in range(T)]
x6 = [0 for i in range(T)]
y4 = [0 for i in range(T)]
y5 = [0 for i in range(T)]
y6 = [0 for i in range(T)]

for i in range(T):
  x4[i],y4[i] = Eye(x1[i]+b,y1[i],-h)
  x5[i],y5[i] = Eye(x2[i]+b,y2[i],-h)
  x6[i],y6[i] = Eye(x3[i]+b,y3[i],-h)
  
"""
for i in range(T):
  x1[i] = Eye(x1[i]+b,y1[i],-h)[0]
  y1[i] = Eye(x1[i]+b,y1[i],-h)[1]
  x2[i] = Eye(x2[i]+b,y2[i],-h)[0]
  y2[i] = Eye(x2[i]+b,y2[i],-h)[1]
  x3[i] = Eye(x3[i]+b,y3[i],-h)[0]
  y3[i] = Eye(x3[i]+b,y3[i],-h)[1]
"""
# axesに散布図を設定する
ax.set_aspect("equal")
"""
ax.scatter(x1, y1, s=0.3, c='g')
ax.scatter(x2, y2, s=0.5, c='r')
ax.scatter(x3, y3, s=0.3, c='b')
"""
ax.scatter(x4, y4, s=0.3, c='g')
ax.scatter(x5, y5, s=0.5, c='r')
ax.scatter(x6, y6, s=0.3, c='b')
ax.set_aspect("equal")
ax.set_ylim(-1.1,0.3)
# 表示する
plt.show()

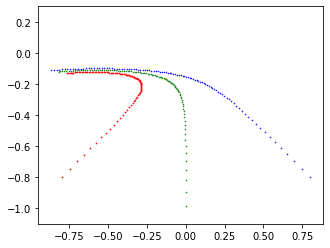
f:id:medical-science:20220228005823p:plain — 見え方

クロソイド曲線を走っていると、だんだんと先が見えない。

前に車や障害物があるかもしれないが、それが遠くては見えない。

スピードを出し過ぎず、安全な速度で、前方を確認しながらハンドルを切ろうね。

バイバイ！