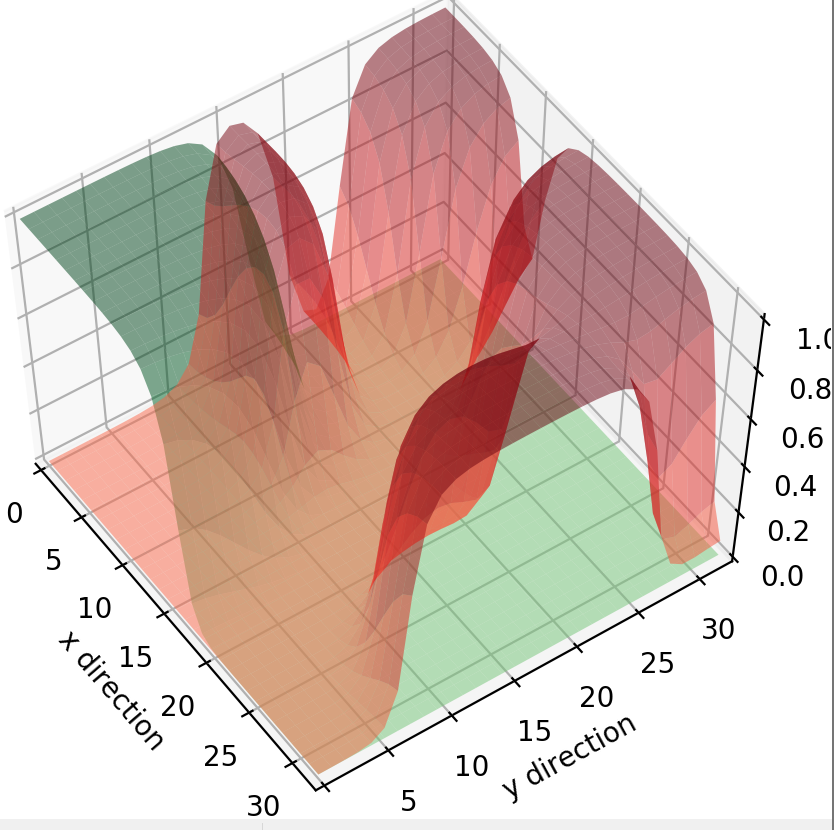
Phase field法なる手法を使えば、2相の境界を上手い具合に図示できるらしい。
それを利用して、A0相とA1相がある状況と、B0相とB1相がある状況を考えて、A0相からA1相に境界近辺で変化しつつ、B0相からB1相でもその境界付近で変化しつつ、B1相はA1相とは共存しがたいため、B0相になっていく。ということを表現できそう。
コードだが、はてなブログの仕様によって、記事に※が入ってしまう問題がある。これの解決策がわからない。編集時点では、そんなことはないのだが、、、。
”””
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
import math
nx,ny=32,32;dx,dy=0.5e-6,0.5e-6;
eee=1.0e+6;sigma=1.0;delta=4.*dx;amobi=4.e-14
ram=0.1;bbb=2.*np.log*1/(1.-(1.-2.*ram)))/2.
aaa=np.sqrt(3.*delta*sigma/bbb);www=6.*sigma*bbb/delta;
pmobi=amobi*math.sqrt(2.*www)/(6.*aaa)
dt=dx*dx/(5.*pmobi*aaa*aaa)/2;nsteps=500
p= np.zeros*2;q=np.zeros*3
r_nuclei=5.*dx
for i in range(0,nx):
for j in range(0,ny):
rp = np.sqrt( (i *dx)**2 +(j*dy)**2 ) - r_nuclei
rq1=np.sqrt( (i *dx-30.*dx)**2 +(j*dy-20.*dy)**2 ) - 0.3*r_nuclei
rq2=np.sqrt( (i *dx-16.*dx)**2 +(j*dy-30.*dy)**2 ) - 0.3*r_nuclei
rq3=np.sqrt( (i *dx-10.*dx)**2 +(j*dy-4.*dy)**2 ) - 0.3*r_nuclei
rq4=np.sqrt( (i *dx-32.*dx)**2 +(j*dy-1.*dy)**2 ) - 0.3*r_nuclei
p[0,i,j] = 0.5*(1.-np.tanh(np.sqrt(2.*www)/(2.*aaa)*rp))
q[0,i,j] = max(0.5*(1.-np.tanh(np.sqrt(2.*www)/(2.*aaa)*rq1)),0.5*(1.-np.tanh(np.sqrt(2.*www)/(2.*aaa)*rq2)),0.5*(1.-np.tanh(np.sqrt(2.*www)/(2.*aaa)*rq3)),0.5*(1.-np.tanh(np.sqrt(2.*www)/(2.*aaa)*rq4)))
def do_timestep(p,q):
for t in range(nsteps-1):
p1=np.zeros*4;p2=np.zeros*5;p3=np.zeros*6;p4=np.zeros*7;
q1=np.zeros*8;q2=np.zeros*9;q3=np.zeros*10;q4=np.zeros*11;
for j in range(ny):
for i in range(nx):
ip=i+1;im=i-1;jp=j+1;jm=j-1;
if ip > nx - 1:
ip = nx -1
if im < 0:
im = 0
if jp > ny - 1:
jp = ny -1
if jm < 0:
jm = 0
# p[t+1,i,j] = p[t,i,j] + pmobi * ( 4.*www*p[t,i,j]*(1.-p[t,i,j])*(p[t,i,j]-0.5+3./(2.*www)*eee)+ aaa*aaa**12+ aaa*aaa**13+ aaa*aaa**14*(p[t,i,j]+p1[i,j]/2-0.5+3*(p[t,i,j]+p1[i,j]/2)*(1-(p[t,i,j]+p1[i,j]/2)))+ aaa*aaa**15*(q[t,i,j]+q1[i,j]/2-0.5-6*(p[t,i,j]+p1[i,j]/2-q[t,i,j]+q1[i,j]/2)*(q[t,i,j]+q1[i,j]/2)*(1-(q[t,i,j]+q1[i,j]/2)))+ aaa*aaa**16*(p[t,i,j]+p2[i,j]/2-0.5+3*(p[t,i,j]+p2[i,j]/2)*(1-(p[t,i,j]+p2[i,j]/2)))+ aaa*aaa**17*(q[t,i,j]+q2[i,j]/2-0.5-6*(p[t,i,j]+p2[i,j]/2-q[t,i,j]+q2[i,j]/2)*(q[t,i,j]+q2[i,j]/2)*(1-(q[t,i,j]+q2[i,j]/2)))+ aaa*aaa**18*(p[t,i,j]+p3[i,j]-0.5+3*(p[t,i,j]+p3[i,j])*(1-(p[t,i,j]+p3[i,j])))+ aaa*aaa**19*(q[t,i,j]+q3[i,j]-0.5-6*(p[t,i,j]+p3[i,j]-q[t,i,j]+q3[i,j])*(q[t,i,j]+q3[i,j])*(1-(q[t,i,j]+q3[i,j])))+ aaa*aaa*((q[t,ip,j]+q3[ip,j] - 2*(q[t,i,j]+q3[i,j]) + q[t,im,j]+q3[im,j])/dx/dx + (q[t,i,jp]+q3[i,jp] - 2*(q[t,i,j]+q3[i,j])+ q[t,i,jm]+q3[i,jm])/dy/dy) ) * dt
for j in range(ny):
for i in range(nx):
# p[t+1,i,j] = p[t,i,j] + pmobi * ( 4.*www*p[t,i,j]*(1.-p[t,i,j])*(p[t,i,j]-0.5+3./(2.*www)*eee)+ aaa*aaa*((p[t,ip,j] - 2*p[t,i,j] + p[t,im,j])/dx/dx + (p[t,i,jp] - 2*p[t,i,j] + p[t,i,jm])/dy/dy) ) * dt
p[t+1,i,j] = p[t,i,j] +(p1[i,j]+p2[i,j]*2+p3[i,j]*2+p4[i,j])/6
q[t+1,i,j] = q[t,i,j] +(q1[i,j]+q2[i,j]*2+q3[i,j]*2+q4[i,j])/6
do_timestep(p,q)
x = np.linspace(0, nx, nx);y=np.linspace(0, ny, ny)
x, y = np.meshgrid(y, x)
fig = plt.figure()
fig.set_dpi(100)
ax = Axes3D(fig)
def animate(i):
ax.clear();
plt.ylim([0,ny]);plt.xlim([0,nx])
plt.xlabel('x direction');plt.ylabel('y direction')
ax.plot_surface(x, y, p[i,:,:], rstride=1, cstride=1, cmap=plt.cm.Greens,alpha=0.5,vmax=1,vmin=-1)
ax.plot_surface(x, y, q[i,:,:], rstride=1, cstride=1, cmap=plt.cm.Reds,alpha=0.5,vmax=1,vmin=-1)
ax.set_zlim(0, 1)
anim = animation.FuncAnimation(fig,animate,frames=nsteps-1,interval=10,repeat=True)
plt.show()
”””
*1:1.+(1.-2.*ram
*2:nsteps,nx,ny
*3:nsteps,nx,ny
*4:nx,ny
*5:nx,ny
*6:nx,ny
*7:nx,ny
*8:nx,ny
*9:nx,ny
*10:nx,ny
*11:nx,ny
*12:p[t,ip,j] - 2*p[t,i,j] + p[t,im,j])/dx/dx + (p[t,i,jp] - 2*p[t,i,j] + p[t,i,jm])/dy/dy) ) * dt
p1[i,j] = pmobi * ( 4.*www*p[t,i,j]*(1.-p[t,i,j])*(p[t,i,j]-0.5+3*p[t,i,j]*(1-p[t,i,j]
*13:p[t,ip,j] - 2*p[t,i,j] + p[t,im,j])/dx/dx + (p[t,i,jp] - 2*p[t,i,j] + p[t,i,jm])/dy/dy) ) * dt
q1[i,j] = pmobi * ( 4.*www*q[t,i,j]*(1.-q[t,i,j])*(q[t,i,j]-0.5-6*(p[t,i,j]-q[t,i,j])*q[t,i,j]*(1-q[t,i,j]
*14:q[t,ip,j] - 2*q[t,i,j] + q[t,im,j])/dx/dx + (q[t,i,jp] - 2*q[t,i,j] + q[t,i,jm])/dy/dy) ) * dt
for j in range(ny):
for i in range(nx):
ip=i+1;im=i-1;jp=j+1;jm=j-1;
if ip > nx - 1:
ip = nx -1
if im < 0:
im = 0
if jp > ny - 1:
jp = ny -1
if jm < 0:
jm = 0
# p[t+1,i,j] = p[t,i,j] + pmobi * ( 4.*www*p[t,i,j]*(1.-p[t,i,j])*(p[t,i,j]-0.5+3./(2.*www)*eee)+ aaa*aaa*((p[t,ip,j] - 2*p[t,i,j] + p[t,im,j])/dx/dx + (p[t,i,jp] - 2*p[t,i,j] + p[t,i,jm])/dy/dy) ) * dt
p2[i,j] = pmobi * ( 4.*www*(p[t,i,j]+p1[i,j]/2)*(1.-(p[t,i,j]+p1[i,j]/2
*15:p[t,ip,j]+p1[ip,j]/2 - 2*(p[t,i,j]+p1[i,j]/2) + p[t,im,j]+p1[im,j]/2)/dx/dx + (p[t,i,jp]+p1[i,jp]/2 - 2*(p[t,i,j]+p1[i,j]/2)+ p[t,i,jm]+p1[i,jm]/2)/dy/dy) ) * dt
q2[i,j] = pmobi * ( 4.*www*(q[t,i,j]+q1[i,j]/2)*(1.-(q[t,i,j]+q1[i,j]/2
*16:q[t,ip,j]+q1[ip,j]/2 - 2*(q[t,i,j]+q1[i,j]/2) + q[t,im,j]+q1[im,j]/2)/dx/dx + (q[t,i,jp]+q1[i,jp]/2 - 2*(q[t,i,j]+q1[i,j]/2)+ q[t,i,jm]+q1[i,jm]/2)/dy/dy) ) * dt
for j in range(ny):
for i in range(nx):
ip=i+1;im=i-1;jp=j+1;jm=j-1
if ip > nx - 1:
ip = nx -1
if im < 0:
im = 0
if jp > ny - 1:
jp = ny -1
if jm < 0:
jm = 0
# p[t+1,i,j] = p[t,i,j] + pmobi * ( 4.*www*p[t,i,j]*(1.-p[t,i,j])*(p[t,i,j]-0.5+3./(2.*www)*eee)+ aaa*aaa*((p[t,ip,j] - 2*p[t,i,j] + p[t,im,j])/dx/dx + (p[t,i,jp] - 2*p[t,i,j] + p[t,i,jm])/dy/dy) ) * dt
p3[i,j] = pmobi * ( 4.*www*(p[t,i,j]+p2[i,j]/2)*(1.-(p[t,i,j]+p2[i,j]/2
*17:p[t,ip,j]+p2[ip,j]/2 - 2*(p[t,i,j]+p2[i,j]/2) + p[t,im,j]+p2[im,j]/2)/dx/dx + (p[t,i,jp]+p2[i,jp]/2 - 2*(p[t,i,j]+p2[i,j]/2)+ p[t,i,jm]+p2[i,jm]/2)/dy/dy) ) * dt
q3[i,j] = pmobi * ( 4.*www*(q[t,i,j]+q2[i,j]/2)*(1.-(q[t,i,j]+q2[i,j]/2
*18:q[t,ip,j]+q2[ip,j]/2 - 2*(q[t,i,j]+q2[i,j]/2) + q[t,im,j]+q2[im,j]/2)/dx/dx + (q[t,i,jp]+q2[i,jp]/2 - 2*(q[t,i,j]+q2[i,j]/2)+ q[t,i,jm]+q2[i,jm]/2)/dy/dy) ) * dt
for j in range(ny):
for i in range(nx):
ip=i+1;im=i-1;jp=j+1;jm=j-1;
if ip > nx - 1:
ip = nx -1
if im < 0:
im = 0
if jp > ny - 1:
jp = ny -1
if jm < 0:
jm = 0
# p[t+1,i,j] = p[t,i,j] + pmobi * ( 4.*www*p[t,i,j]*(1.-p[t,i,j])*(p[t,i,j]-0.5+3./(2.*www)*eee)+ aaa*aaa*((p[t,ip,j] - 2*p[t,i,j] + p[t,im,j])/dx/dx + (p[t,i,jp] - 2*p[t,i,j] + p[t,i,jm])/dy/dy) ) * dt
p4[i,j]=pmobi*(4.*www*(p[t,i,j]+p3[i,j])*(1.-(p[t,i,j]+p3[i,j]
*19:p[t,ip,j]+p3[ip,j] - 2*(p[t,i,j]+p3[i,j]) + p[t,im,j]+p3[im,j])/dx/dx + (p[t,i,jp]+p3[i,jp] - 2*(p[t,i,j]+p3[i,j])+ p[t,i,jm]+p3[i,jm])/dy/dy) ) * dt
q4[i,j]=pmobi*(4.*www*(q[t,i,j]+q3[i,j])*(1.-(q[t,i,j]+q3[i,j]