球面とその周りに血管を貼る、スターフルーツ
まずは、こちらの記事と、こちらの記事を参考に球面を表示する。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# データ生成していく、u,vで2つの自由度持たせている。
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
#numpy.outerを使っているのは、u,vの2つの自由度を持たせたら、行列になる。
#なので、行列を作るために、2つのリスト(ベクトル)の外積を取った
x = 10 * np.outer(np.cos(u), np.sin(v))
y = 10 * np.outer(np.sin(u), np.sin(v))
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v))
#表面を表示する・プロットしていく
plt.savefig("3d_ball.jpg",dpi=120)
plt.show()

続いて、肺胞などをイメージすると、肺胞の周りに毛細血管が覆っていて、ガスを交換している。かたちについては、球体の周りに筒が張り付いている。
それを少し真似た図を作る。
筒が張り付いているとはいえ、球面にある程度接着して張り付いているので、結合組織なども考慮すれば、球面と筒は連続的として良さげ。(ただし、導関数が連続とは限らない)
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
def near(r,a,epsilon):# a と epsilon の近さに応じて重みをつけるための関数
return abs(r-a-epsilon)+abs(r-a+epsilon)
epsilon = 0.05
# データ生成していく、u,vで2つの自由度持たせている。
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
#追加
a = np.pi*3/8
#numpy.outerを使っているのは、u,vの2つの自由度を持たせたら、行列になる。
#なので、行列を作るために、2つのリスト(ベクトル)の外積を取った
x = 10 * np.outer(np.cos(u), np.sin(v) + 0.2*np.exp(-10*near(v,a,epsilon)**2))
y = 10 * np.outer(np.sin(u), np.sin(v) + 0.2*np.exp(-10*near(v,a,epsilon)**2))
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v) + 0.2*np.exp(-10*near(v,a,epsilon)**2))
#表面を表示する・プロットしていく
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
plt.savefig("3d_ball.jpg",dpi=120)
plt.show()
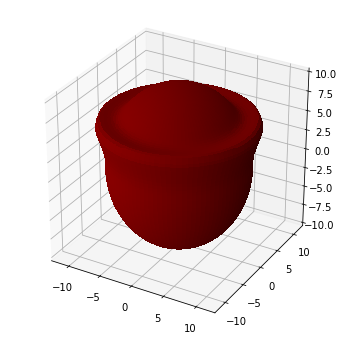
3/8πの部分付近に毛細血管を貼った肺胞。
実際には、多くの毛細血管、そして、形も分岐があったり、曲がったりしている。
時間があればそれをモデリングしたい。
ちなみに、サイクロイドを使うことで周期性を利用した、面白いことが出来る。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# データ生成していく、u,vで2つの自由度持たせている。
u = np.linspace(0, 2 * np.pi, 1000)
v = np.linspace(0, np.pi, 1000)
#numpy.outerを使っているのは、u,vの2つの自由度を持たせたら、行列になる。
#なので、行列を作るために、2つのリスト(ベクトル)の外積を取った
#ちなみに、少し周期を変えることで、サイクロイドのように、周期的にガタガタさせる
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v))
#表面を表示する・プロットしていく
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
plt.savefig("3d_ball.jpg",dpi=120)
plt.show()
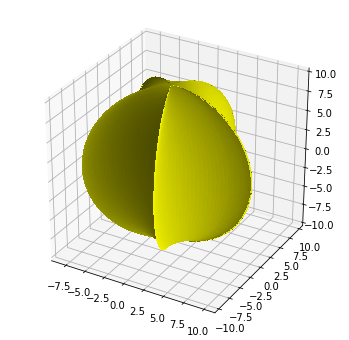
これは、果物のスターフルーツ様である。(本物はもう少しギザギザしているが)
スターフルーツはインドなどの南アジア、熱帯アジアが原産で、熱帯や亜熱帯で栽培される。日本なら沖縄など。
神経毒であるカランボキシンを含んでいるので、腎臓の機能が悪い人は、神経症状が出る。
シュウ酸を微量に含むので、腎機能低下時に、カルシウムと結合してシュウ酸カルシウム結石症になる。
バイバイ!