『感染症疫学のためのデータ分析入門』

こちらの本をまとめる。お絵かきする。

  • 感染と感染のメカニズムと疫学的指標
    • 疫学とは、人の集団を対象とした健康や疾病に関する学問
    • 人の集団の健康に関する状況や事象の分布やリスクの規定因子、影響を及ぼす規定因子（Determinants）の研究、健康問題を制御するために疫学を応用すること。
    • 症例がリスク因子（感染者は保有者、スプレッダー）
    • 接触様式
    • 免疫と経験（ワクチン予防接種、獲得免疫）
    • 緊急性
    • 感染
      • 微生物（細菌、ウイルス、真菌、原虫）
      • 感染源に暴露されて、4通り
        • キャリア、不顕性感染、顕性感染、感染なし
      • その後の経過について、
        • 死亡、キャリア、免疫獲得、免疫不獲得
      • コッホの条件（見える、培養可能、打ったら発症、打って発症したら見える）
      • 疫学三角（病因、宿主、環境）
        • その特徴に合わせて、対策を打つ。
      • 致命リスク、感染時致命リスク。
      • インデックス・ケース（最初の特定されたケース）
      • n次感染
      • エピデミックは一定期間に同一の感染者が通常に比べて高い頻度で発生すること。
        • それと比べて、ある地域で同一の感染症が常在的に発生することを、エンデミックという。
        • エピデミックは高いとき、エンデミックは普通
      • ある地域で同一の感染症が持続的に高いレベルで発生することを、ハイパーエンデミックという。
      • パンデミックは、一定期間をまたいで、世界的に広範囲で同一の感染症が流行すること。
  • 感染症の自然史
    • 診断バイアスとは、診断と報告が行われずに感染者数が低く見積もられる問題。
      • 不顕性感染とか、受診しない意志、医療の誤診断など。
    • 時間経過
      • 潜伏期間（感染してから、発症するまで）
      • 世代間隔
      • 感染性待ち期間（感染してから、感染性を獲得するまで）
    • 単一暴露流行における暴露時刻の推定

 

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import math
def log_normal_distribution(t, mu, gamma, sigma):#対数正規分布
child = math.exp(-(math.log(t-gamma)-mu)**2/(2*sigma**2))
  return child/*1

data = [1,6,53,45,34,14,10,10,3,2]
Sum = sum(data)
T = len(data)

def check_distance(mu,gamma,sigma):
  answer = 0
  scale = sum([log_normal_distribution(t,mu,gamma,sigma) for t in range(T)])/Sum
  for t in range(T):
    answer += (data[t]*scale- log_normal_distribution(t,mu,gamma,sigma))**2
  return answer

def calc_mu_sigma(gamma):
  answer2 = [math.log(t-gamma) for t in range(T)]
  new_mu = sum(answer2)/T
  new_sigma = math.sqrt(sum([answer2[i]**2 for i in range(T)])/T - new_mu**2)
  return (new_mu,new_sigma)


cost = 10**10
candidate = (1,1,1)
for gamma in range(-100, 0, 1):
  (mu,sigma) = calc_mu_sigma(gamma)
  now_cost = check_distance(mu, gamma/100, sigma)
  #print(cost)
  if now_cost<= cost:
    cost = now_cost
    candidate = (mu, gamma/100, sigma)
print(candidate)

estimated_gamma = candidate[1]
print("gamma=",estimated_gamma+12)
  • 感染症と重篤度の評価
    • 基本再生産数とは、集団内の全てのものが感受性を有する時に、1人の感染者が生み出す2次感染者数の平均値。
    • 予防接種は、感受性をもつ人を減らす。
    • 死亡率＝罹患率×致命リスク
  • アウトブレイク調査：能動的サーベイランス
    • サーベイランスは、情報収集して、解析して、監視していくこと。
    • 時、場所、人、流行曲線（時間、場所のパラメータ）
    • B型肝炎ウイルスとバネ式器具の使用歴
      • Fisherの正確検定。こちら。極端な例の確率を取り出して集めることで、p値にする。
data = [25,32,0,5]
extreme_data = [20,37,5,0]

def Factor(n):
  answer = 1
  if n<=1:
    return 1
  else:
    for i in range(2,n+1):
      answer *= i
    return answer


def Fisher(data):
  n = len(data)
 child1 = Factor(data[0]+data[1])*Factor(data[0]+data[2])
child2 = Factor(data[1]+data[3])*Factor(data[2]+data[3])
 mother = Factor(data[0])*Factor(data[1])*Factor(data[2])*Factor(data[3])
  return child1*child2/(mother*Factor(sum(data)))

p = Fisher(data)+Fisher(extreme_data)
 
  • 感染者割合の推定
    • 感染者割合の分析
    • 診断検査データを活用した推定
    • 逆計算法を使用した推定
    • 捕獲再捕獲法
  • 予防接種の評価
    • コンパートメントモデル
  • 受動的サーベイランスとそのデータ分析
    • 収集、照合、解析と解釈、普及と利用
  • アウトブレイクの早期検出
    • 検出閾値の決定方法
      • 回帰
        • Stroupの方法
data = [100, 200, 125]

mu = sum(data)/len(data)
sigma = sum([data[i]**2 for i in range(len(data))])/len(data) - mu**2
real_sigma = len(data)*sigma/(len(data)-1)

def Stroup_check(new_data):
  half_length = 1.96 * (real_sigma * (len(data)+1)/len(data))**0.5
  if mu - half_length <= new_data <= mu + half_length:
    print("no statistical difference")
  else:
    print("statisical difference")

Stroup_check(240)
        • 時系列傾向と季節性を加味したモデル。 E(Y;t) = \alpha+\beta t+ \gamma cos(\omega t + \phi)
        • これまでは、観察データのバラツキが正規分布に従う前提。
        • イベントの頻度が低い場合は、ポアソン分布
        • Farringtonらによる、CDSCのモデルもポアソン分布への近似変換を利用
      • 時系列分析
        • 指数平滑化
      • 統計的プロセス制御法
        • 累積和
      • 地理情報を組み込んだ技法
        • spatial cumsum統計量
  • 感染症数理モデル入門
    • コンパートメントモデル
    • SIRモデル、元に戻れない、という点で、癌の変異とかの話にも転用できそう。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import math


T = 1000
S = [-1]*T
I = [-1]*T
R = [-1]*T
#S = [-1]
#I = [-1]
#R = [-1]
###initial condition###
s_temp = 0.999
i_temp = 0.001
r_temp = 0
beta = 0.3
gamma = 0.1
s = [0] * T
i = [0] * T
r = [0] * T
s[0] = s_temp
i[0] = i_temp
r[0] = r_temp


for t in range(T-1):
    #S = S+[-beta * S[i] * I[i]]
    #I = I+[(beta * S[i] * I[i] - gamma * I[i])]
    #R = R+[(gamma * I[i])]
    s_temp = -beta * s_temp * i_temp + s_temp
    #print(s_temp)
    i_temp = beta * s_temp * i_temp - gamma * i_temp + i_temp
    r_temp = gamma * i_temp + r_temp
    s[t+1] = s_temp
    i[t+1] = i_temp
    r[t+1] = r_temp
    #print(s_temp,r_temp)


  

import matplotlib.pyplot as plt
 
# プロット範囲のxを用意
time = [k for k in range(T)]
# x = array([-5, -4, -3, -2, -1,  0,  1,  2,  3,  4,  5])
 
# xに対応するyの値を用意
#y = x**3
 
# pyplot.plot(x, y)でプロット作成
plt.plot(time, s, "r--")
plt.plot(time, i, "g*")
plt.plot(time, r, "b")
 
# plt.show()で画面に表示
plt.show()

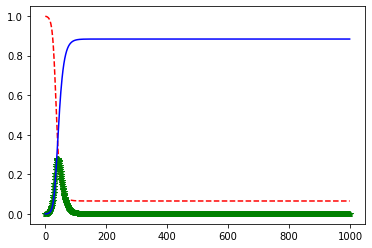
f:id:medical-science:20211217121402p:plain

 

  • 流行のモニタリング

    • 報告が遅れるので、たたみ込みの式になる。
    • 輸入感染例と国内感染例がある。国内感染例は全感染例からのたたみ込み。
  • 2次感染のバラつきと流行発生確率
    • 二次感染のバラツキ
      • スーパースプレッダー
    • 大規模流行の確率
      • 分岐過程モデル
        • 子孫の分布確率
        • 絶滅確率
      • 輸入感染者による流行確率
      • 移動制限
    • 流行収束

一旦これで止めておく。

バイバイ！

*1:t-gamma)*sigma*math.sqrt(2 *math.pi