『遺伝統計学の基礎』の第2章

こちらの本に引き続き入門する。

DNA、RNA、タンパク質、形質。

  • DNA2重鎖
    • 染色体
      • DNA分子とタンパク質からなる
      • DNA分子
        • 4種類の塩基が一列に並ぶ、連なる
        • 配列が情報となる
        • 2重であること
          • AとT、GとCというペアがある。
          • 片方の配列に、もう片方が対応する。
          • メリット
            • バックアップ
            • 逆向きもすぐに取り出せる
    • 複製、変異、組換え
      • 複製
      • 変異
        • 体細胞変異
        • 生殖細胞変異
          • 背景にある考え方は、体細胞と、生殖細胞の2種類で、排反であるということ（憶測）
      • 組換え
        • 精子・卵子に染色体を渡す時、一本分、の染色体を渡す
          • 一本、だと、そのまま分けるイメージだが、実際は継ぎ接ぎして出来ているので、分、がつく。
          • この継ぎ接ぎを組換えという。
    • 起源が同じーIBD
      • 親が2つ持っているアレル
      • そのうち1つを受け継ぐ
      • これを父と母の両方でする
      • アレルの起源が同じであることを、IBDという。
      • 一卵性双生児はIBD数は2、親子は1、同胞は確率的に0か1か2か。
    • 1つの数値で表して扱い安くするーIBDの期待値
      • 期待値で表すと、分布の情報が失われる。
      • 平均、分散、モーメント、期待値
        • モーメント
          • cを中心としたk次のモーメント
    • 同胞のアレルの一致率
    • 染色体の長さがバラバラ
      • 染色体の長さが等しいモデルと等しくない（実際）モデル
      • プロットすると、等しい方は、階段状になる。
      • 教訓（気をつけること）
        • データをプロットすること
        • 特別な条件
        • 離散的な性質

お絵かきする

 

import matplotlib.pyplot as plt
import numpy as np
import math
import random

def moment(x,p,c,k):
    if len(x)==len(p):
        return sum([p[i]*(x[i]-c)**k for i in range(len(p))])
    else:
        return None
def ave(x):
    return sum(x)/len(x)

data = [1,2,3]
prob = [0.2,0.3,0.5]
mom = moment(data,prob,2,ave(data))
print(mom)

def factorial(n):
    if n==0:
        return 1
    elif n==int(n) and n>0:
        fac = 1
        for i in range(1,n):
            fac*=(i+1)
        return fac

def combination(n,i):
    return factorial(n)/(factorial(i)*factorial(n-i))

def allele(k,i):
    return combination(2*k,i)/2**(2*k)

def plot_allele():
    k=23
    num_match=[i for i in range(2*k+1)]
    prob_match=[]
    for i in range(2*k+1):
        prob_match.append(allele(k,i))
    plt.plot(num_match, prob_match)
    plt.xlabel("number of match")
    plt.ylabel("probability")
    plt.title("Allele match",color="red")
    plt.show()

plot_allele()

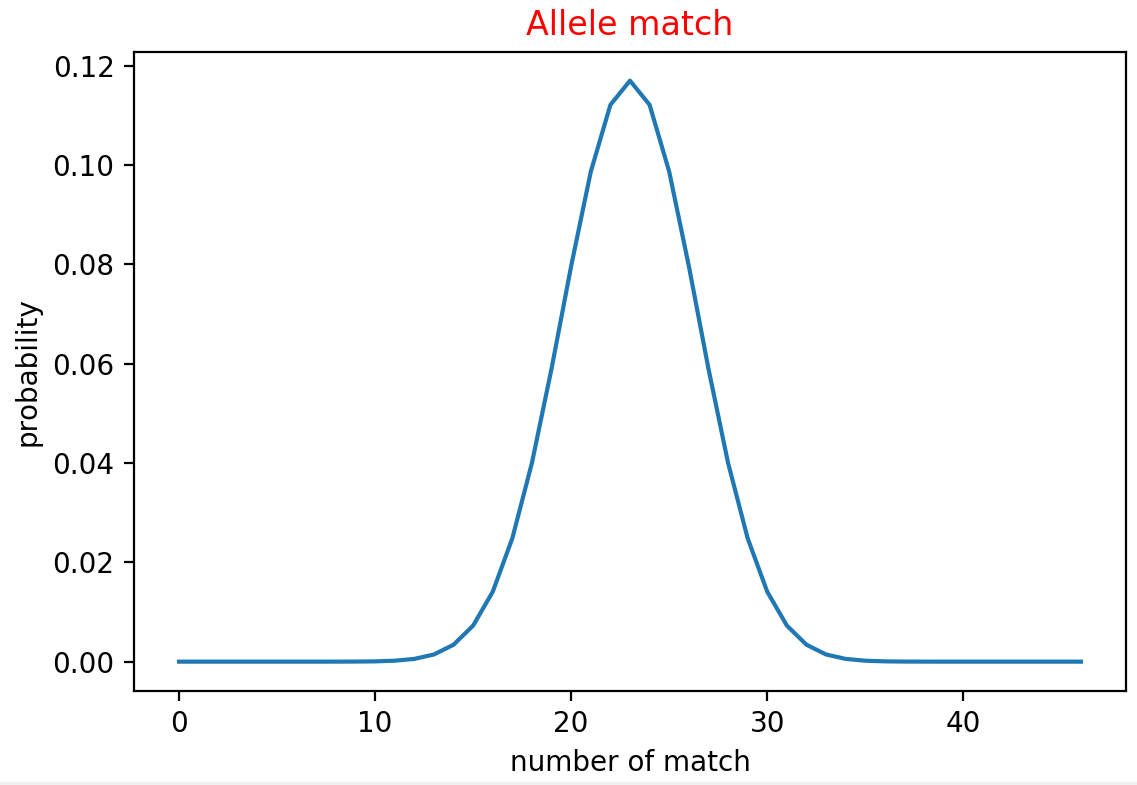
f:id:medical-science:20220408170139p:plain

 

    • 染色体は23対よりももっと細かくなるーー交叉、組換え：ポアッソン過程と指数分布
      • 交叉が起こることは非常にレア。
        • レアなことが起こる時の分布として、ポアッソン分布がある。
          • 何回中××回○○が起こること。
          • その××を固定して、試行回数を無限に飛ばすと、ポアソン分布
        • 交叉間距離が指数分布になるらしい。
          • サイコロを振って6が出ないことが続いていく様子が指数分布になっているのと同じこと？？

データはプロットしてみなさい。という教訓があったので、お絵かきしてみる。

#initial settings
L=10000;r=0.0001;N=1000
#function settings
def poisson(l,k):
    return l**k/factorial(k)*math.exp(-l)

#poisson分布を頑張って作る
#xの時の確率は分かった。
m=135
poisson_data=[0]*m
poisson_data[0]=poisson((L-1)*r,0)
for i in range(m-2):
    poisson_data[i+1]=poisson_data[i]+poisson((L-1)*r,i+1)
poisson_data[-1]=1

#確率がわかった上で、そこからサンプリングするようにしたい
#二分探索で絞り込むことで、確率分布の逆関数チックなことをしている。
def binary_search(x,data):
    l=0;r=len(data)
    while r-l>1:
        mid=(l+r)//2
        if x>=data[mid]:
            l=mid
        else:
            r=mid
    return l

def main():
    random_data=[random.random() for i in range(N)]
    data=[0]*m
    cnt=[i for i in range(m)]
    for i in range(N):
        num=binary_search(random_data[i],poisson_data)
        data[num]=data[num]+1
    plt.plot(cnt,data,color="green")
    plt.xlabel("number of cross")
    plt.ylabel("prob")
    plt.show()

main()

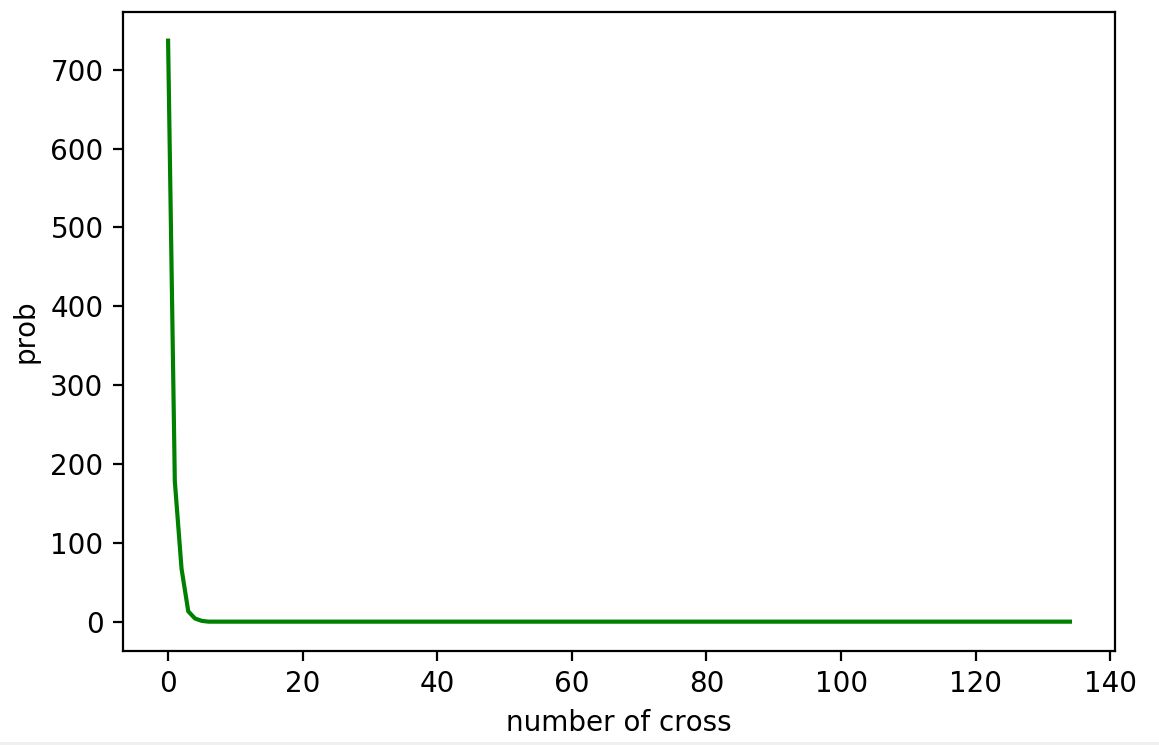
f:id:medical-science:20220408182732p:plain

  • DNAからRNA、タンパク質へ
    • DNAからRNAへー転写
      • DNAからRNAへ情報を転送する（情報を載せる物質を変える）
      • Tの代わりにUを使う。
      • 機能：タンパク質に翻訳される用、その他RNAとして何かする
    • RNAからタンパク質へー翻訳
      • mRNAの情報から、アミノ酸配列（タンパク質）を作ること
      • 3つずつの塩基の組が、アミノ酸に対応する。
        • この組をコドンという
          • 開始コドン、終止コドン

バイバイ！（←この記事の終止コドン）